Uma função f:IR→IR é denominada função do 1º grau na variável independente x, quando for da forma y = f(x) = ax + b
onde a e b são números reais, com a≠0. Exemplos:
- f(x)=7x - 3 , onde a=7 e b=-3
- y = -4x + 3 , onde a=-4 e b=3
O gráfico de uma função do primeiro grau, na variável real x, representado no plano cartesiano, é uma reta não paralela ao eixo das abscissas.

Numa função do 1º grau f: IR→IR definida por y=f(x)=ax+b, temos seguintes elementos: a: coeficiente angular; b: coeficiente linear.
O sinal do coeficiente angular indica se a função é crescente ou decrescente: a>0: função crescente; a<0: função decrescente. Exemplos:
- A função y=2x - 3 é crescente,pois a=2>0
- A função y=-x + 3 é decrescente, pois a=-1<0
Então, o coeficiente de x indica o crescimento ou decrescimento da função, logo o termo independente de x, indica onde a reta corta o eixo y.
Sinal de uma Função do 1º grau
O sinal de uma funçao do 1º grau corresponde ao sinal do y.
Exemplo: estudar o sinal da função definida em IR, por y = 2x - 4.
resolução:
- Achemos o "zero da função":
y=0 => 2x - 4 =0 => 2x = 4 => x = 2
- Esboçamos o gráfico da função. Observe que o gráfico contém o ponto (2;0) e é uma função crescente:
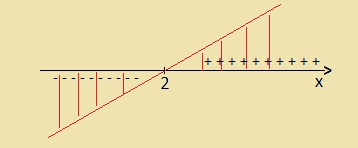
- Pelo gráfico podemos dizer que:
y = 0 para x = 2
y > 0 para x >2
y < 0 para x < 2
Função Linear
Uma função f: IR → IRda forma y = f(x) = ax, com a є IR e a ≠ 0, é uma função linear.
Toda função do primeiro grau y = ax + b em q o termo independente de x (b) é igual a zero é tam bem chamada de função linear.
- Observação 1: uma função linear é um caso particular de uma função do primeiro grau.
- Observação 2: Como a função linear é funçao do primeiro grau, o gráfico tambem será uma reta.
A diferença é que a reta intercepta os dois eixos coordenados na origem. Lembre: em relação à função do primeiro grau o termo independente de x (b) indica onde a reta corta o eixo y. Como na função linear temos b = 0, então a reta correspondente interceptará o eixo y, no ponto (0;0).
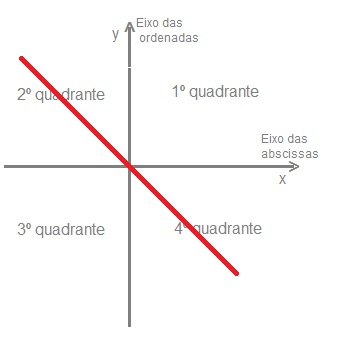
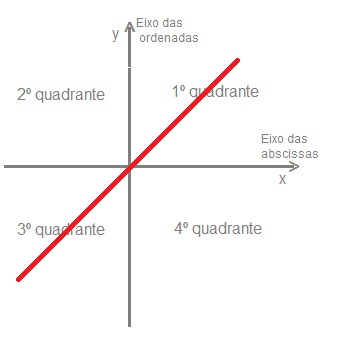
Bissetriz: Uma bissetriz é uma reta que divide um ângulo ao meio. Assim temos duas bissetrizes que nos interessam no plano cartesiano:
- A bissetriz dos quadrantes ímpares - É reta que divide ao meio o 1º e o 3º quadrante.
- A bissetriz dos quadrantes Pares - É reta que divide ao meio o 2º e o 4º quadrante.